【Day 24】回歸器 Regressor 與分類器 Classifier

15th鐵人賽機器學習回歸器分類器

許皓翔

團隊最強資工大電神

2023-10-09 22:28:44

550 瀏覽

分享至

前言

在前面【Day 6】回歸與分類 Regression & Classification 的文章中，了解到我們用模型主要來處理的問題任務，也就是回歸問題與分類問題，若想要詳細了解這兩種問題可以參考 Day 6 的內容，那今天我們就要針對這兩個問題下的模型做介紹，用來處理回歸問題的模型我們通稱回歸器 ( Regressor ) ，處理分類問題的模型通稱為分類器 ( Classifier )。

回歸器 ( Regressor )

回歸器，就是用來解決回歸問題的模型，此部份提到的模型皆指回歸器，當面對到回歸問題時，在訓練模型時所使用的資料，其標籤 ( 模型要去預測的 Target ) 為一連續變數 ( Continuous Variable )，代表我們可能會用模型去預測「能用測量或計算方法取的數值」，包括身高體重，房價等，因此具備預測數值功能的模型就叫做回歸器，而依據預測方式的不同，就有不同的回歸器如下：

簡單線性回歸 ( Simple Linear Regression )
多元線性回歸 ( Multiple Linear Regression )
多項式回歸 ( Polynomial Regression )

線性回歸

線性回歸模型其實就是一個線性函數，這個簡單線性的函數大家一定都看過，如下：

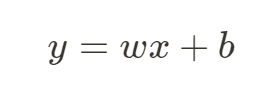
上面式子構成了基本的簡單線性回歸模型， $y$ 為模型的最終輸出， $w$ 就是模型的參數 ( Weight )， $x$ 為輸入的特徵資料， $b$ 為偏差 ( bias )，由此可知這個函數輸入的 $x$ 只有一個，代表輸入至模型的特徵數量為 1，整個函數就為一個單變數函數，自變數為 $x$ ( 特徵 )，應變數為 $y$ ，而依據資料中特徵數量的不同，線性回歸模型可分為簡單線性回歸 ( Simple Linear Regression ) 與多元線性回歸 ( Multiple Linear Regression )，只有一個特徵時，屬於簡單線性回歸模型，若有多個特徵 ( 大於 1 ) 時則屬多元線性回歸模型：

簡單線性回歸 ( Simple Linear Regression )：

傳入模型的特徵 $x$ 只有一個 ( 獨立變數 )，因此模型的輸出為輸入為單變數函數 $y(x)$ ，此函數即為簡單線性回歸模型
多元線性回歸 ( Multiple Linear Regression )：

若傳入模型的特徵 $x$ 不只一個，可能會有 $x_1,x_2,x_3$ ，其模型輸出為輸入的多變數函數 $y(x_1,x_2,x_3)$ ，此函數即為多元線性回歸模型

下圖就是一個簡單線性回歸模型輸出的表現，紅線為模型函數的輸出，綠色為真實的資料點，X 軸為自變數 ( 特徵 )，Y 軸為模型輸出，而訓練模型的目的就是要讓模型的輸出越接近真實資料點。

多項式回歸

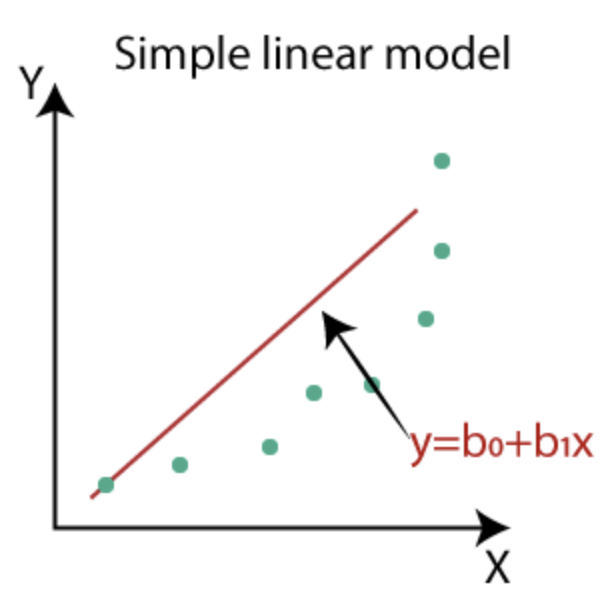
多項式回歸模型顧名思義和多項式有關，上面提到的線性回歸模型是用線性函數，而多項式回歸模型就是利用多項式函數來當作模型架構，提到多項式函數大家一定都不陌生吧，如下：

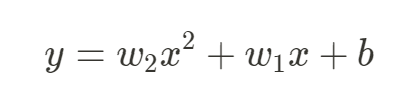
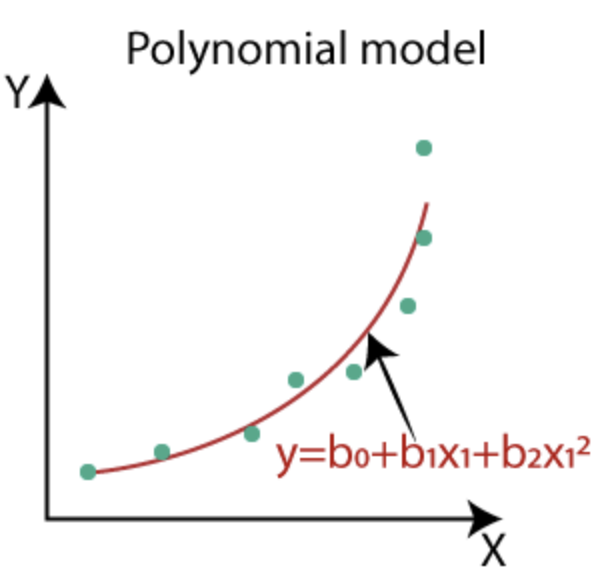
上式就用了二次多項式的函數來表示我們的多項式模型，其傳入的特徵數量為 2，由此可知模型參數的數量會隨著輸入特徵的數量增加而增加，使用多項式函數來當作模型架構的好處是因為其函數的特性，多項式函數能夠通過座標上的任意一點，也就是座標上任一點皆可用多項式函數來表示，因此多項式函數在擬和真實資料上的表現也較線性函數佳 ( 如下圖 )，但對於擬和能力較佳的多項式模型也需要注意過度擬和 ( Overfitting ) 的問題，關於過度擬和的部分在【Day 21】欠缺擬和與過度擬和 Underfitting & Overfitting 有做說明。

分類器 ( Classifier )

分類器就是用來處理分類問題所使用的模型，一個分類問題可以是區分動物的種類，像是你把一張貓的圖片輸入至模型中，模型就會針對這張圖片去進行分類，分類是哪種貓 ( 波斯貓、折耳貓等 … )，因此有這種分類功能的模型就叫做分類器，那既然是分類的問題，資料的標籤即為類別變數，所謂類別變數指的就是一個離散數值，關於這部分詳細介紹可至 Day 6，那分類問題也有分成二元分類和多元分類：

二元分類器

像是要模型依據傳入的特徵資料去預測這個人是否患有糖尿病，這就是個二元分類問題，會將問題的結果分成兩類，為患有糖尿病 與無患有糖尿病 這兩類，通常面對到這種問題，常用的分類器可為邏輯回歸模型 ( Logistic Regression Model )，而邏輯回歸這個二元分類器會將這兩類結果標籤用二進制的角度去詮釋分類，變成真假 ( 1、0 ) 邏輯的問題，關於邏輯回歸的模型會在之後文章詳述。
多元分類器

對於多元分類的問題，像是要對動物的品種做分類等，較常見的分類器則會使用 VGG 模型，可用來做多元的分類，這個多元分類器在之後幾天我們也會帶大家一起實作，使用 VGG 架構的模型意味和卷積神經網路 ( CNN ) 架構有著密切的關係，並且能夠解決相對複雜的分類問題，關於卷積神經網路的介紹也會在之後的文章做詳述。